Acute Angle Between Two Lines

The angle is nothing simply the figure formed by two rays. If two straight lines meet, then they class two sets of angles. The intersection forms a pair of acute angles and another pair of obtuse angles. The angle values will be based on the slopes of the intersecting lines. Bank check out the formula to calculate the angle between 2 directly lines, derivation, example questions with answers in the post-obit sections of this page.

Angle between Two Lines – Definition

In a aeroplane when two straight and non-parallel lines see at a point, then it forms 2 opposite vertical angles. In the formed angles, one is lesser than 90 degrees and the other is greater than 90 degrees. We volition find the bending betwixt two straight and perpendicular lines is 90 degrees and parallel lines is zero degrees.

Bending between 2 Straight Lines Formula and Derivation

Let us consider θ as the angle betwixt two intersecting direct lines. And those directly lines be y = mx + c, Y = MX + C, then the angle θ is given by

tan θ = ± \(\frac { (M – m) }{ (1 + mM)} \)

Derivation

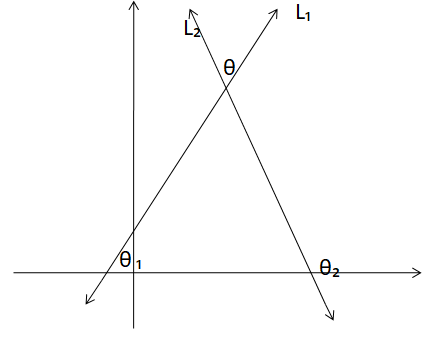
Two straight lines Fifty₁, Fifty₂ are intersecting each other to grade astute and obtuse angles.

Permit us take the slope measurement can exist taken as

tan θ₁ = k₁ and tan θ₂ = m₂

From the figure, we tin say that θ = θ₂ – θ₁

At present, tan θ = tan(θ₂ – θ₁)

tan θ = \(\frac { (tan θ₂ – tan θ₁) }{ (i + tan θ₁ tan θ₂) } \)

Substitute tan θ₁ = m₁, tan θ₂ = k₂

tan θ = \(\frac { (1000₂ – m₁) }{ (i + m₁ thou₂) } \)

How to find Angle Betwixt Two Straight Lines?

If iii points on a coordinate plane are given, then endpoints of a line are (x₁, y₁) and (x₂, y₂)

The equation of the slope is m = \(\frac { (y₂ – y₁) }{ (x₂ – x₁) } \)

m₁ and thou₂ can exist calculated past substituting in the formula, then the angle between two lines is given past

tan θ = ± \(\frac { one thousand₂ – m₁) }{ (one + thou₁ m₂) } \)

Also Check:

Pairs of Angles
Bending of Elevation
Bending of Depression

Bending between Two Directly Lines Examples

Example one:

If A (-2, i), B (ii, 3), and C (-2, -iv) are three points, notice the bending between two straight lines AB, BC.

Solution:

Given that,

3 points are A (-2, ane), B (ii, 3), and C (-ii, -4)

The slope of line AB is m = \(\frac { (y₂ – y₁) }{ (x₂ – x₁) } \)

1000 = \(\frac { (3 – 1) }{ (2 – (-2)) } \)

= \(\frac { (2) }{ (ii + 2) } \)

= \(\frac { 2 }{ 4 } \)

= \(\frac { i }{ 2 } \)

Therefore, m₁ = \(\frac { ane }{ two } \)

The slope of line BC is given past

1000 = \(\frac { (y₂ – y₁) }{ (x₂ – ten₁) } \)

m = \(\frac { (-4 – 3) }{ (-2 – 2) } \)

= \(\frac { -vii }{ -iv } \)

= \(\frac { 7 }{ 4 } \)

Therefore, thousand₂ = \(\frac { 7 }{ 4 } \)

Substituting the values of m2 and m1 in the formula for the angle betwixt two lines when nosotros know the slopes of two sides, we have,

tan θ = ± \(\frac { (yard₂ – m₁) }{ (1 + grand₁ k₂) } \)

= ± \(\frac { (\frac { 7 }{ iv } – \frac { 1 }{ ii } ) }{ (1 + \frac { 1 }{ 2 } * \frac { 7 }{ 4 }) } \)

= ± \(\frac { 2 }{ 3 } \)

Therefore, θ = tan^-1 (⅔)

So, the angle between the lines AB, BC is tan^-1 (⅔).

Case 2:

Observe the angle between the following lines 4x – 3y = 8, 2x + 5y = 4.

Solution:

Given two directly lines are 4x – 3y = 8, 2x + 5y = iv

Converting the given lines into slope intercept form

4x – 3y = eight

4x = eight + 3y

3y = 4x – 8

y = \(\frac { 4x – 8 }{ 3 } \)

y = \(\frac { 4x }{ 3 } – \frac { 8 }{ 3 } \)

Therefore, the gradient of line 4x – 3y = 8 is \(\frac { 4 }{ 3 } \)

2x + 5y = 4

5y = 4 – 2x

y = \(\frac { 4 – 2x }{ 5 } \)

y = \(\frac { -2x }{ v } + \frac { four }{ 5 } \)

Therefore, the slope of the line 2x + 5y = iv is –\(\frac { 2 }{ 5 } \)

The angle between lines is tan θ = ± \(\frac { (g₂ – chiliad₁) }{ (1 + m₁ m₂) } \)

= ± \(\frac { (\frac { -2 }{ five } – \frac { 4 }{ 3 } ) }{ (one + \frac { 4 }{ three } * \frac { (-2) }{ 5 }) } \)

= \(\frac { -26 }{ vii } \)

θ = tan^-1 (\(\frac { -26 }{ 7 } \))

Example 3:

Find the angle between ii lines x + y = four, x + 2y = 3.

Solution:

The given two lines are x + y = iv, x + 2y = iii.

The slope-intercept form of the get-go line is

ten + y = 4

y = iv – x

Therefore, slope of ten + y = 4 is m₁ = -one

The slope-intercept form of the 2nd line is

x + 2y = three

2y = iii – x

y = \(\frac { (3 – x) }{ 2 } \)

y = \(\frac { 3 }{ ii } – \frac { 10 }{ ii } \)

Therefore, slope of x + 2y = 3 is m₂ = \(\frac { -1 }{ ii } \)

The angle between lines is tan θ = ± \(\frac { (m₂ – one thousand₁) }{ (i + yard₁ chiliad₂) } \)

= ± \(\frac { (\frac { -1 }{ 2 } – (-one) ) }{ (one + \frac { -1 }{ ii } * (-1)) } \)

= \(\frac { 1 }{ three } \)

θ = tan^-1(\(\frac { one }{ 3 } \))

Instance iv:

Find the bending between two straight lines x + 2y – i = 0 and 3x – 2y + 5 = 0

Solution:

The given lines are x + 2y – one = 0 and 3x – 2y + 5 = 0

The slope intercept course of showtime line is

10 + 2y – one = 0

2y = ane – 10

y = \(\frac { ane – ten }{ 2 } \)

y = \(\frac { one }{ two } – \frac { ten }{ 2 } \)

Therefore, the slope of line x + 2y – one = 0 is m₁ = \(\frac { -1 }{ ii } \)

The gradient-intercept form of the 2d line is

3x – 2y + 5 = 0

3x + 5 = 2y

y = \(\frac { 3x + 5 }{ two } \)

y = \(\frac { 3x }{ 2 } + \frac { 5 }{ two } \)

Therefore, the slope of line 3x – 2y + v = 0 is 1000₂ = \(\frac { 3 }{ ii } \)

The angle between lines is tan θ = ± \(\frac { (grand₂ – m₁) }{ (1 + m₁ k₂) } \)

= ± \(\frac { (\frac { iii }{ two } – \frac { (-1 }{ 2 )} ) }{ (1 – \frac { 1 }{ ii } * \frac { (3) }{ ii }) } \)

= ii

θ = tan^-ane(2)